关键词： 教师资格证

• *备考没方向？
• *考试时间不清楚？
• *成绩看不懂？
• *考试内容没有掌握？
• *拿证之后何去何从？
• *别人上岸也这么难？

扫码添加专属备考顾问
▪ 0元领取考点真题礼包
▪ 获取1对1备考指导

全国教资备考群：737804026（点击进群，群内定期分享教资备考笔面通关资料包，并有客服老师答疑解惑）

内容：

思考

类似于利用数轴确定直线上点的位置，能不能找到一种办法来确定平面内的点的位置呢（例如图7.1-3中A，B，C，D各点）？

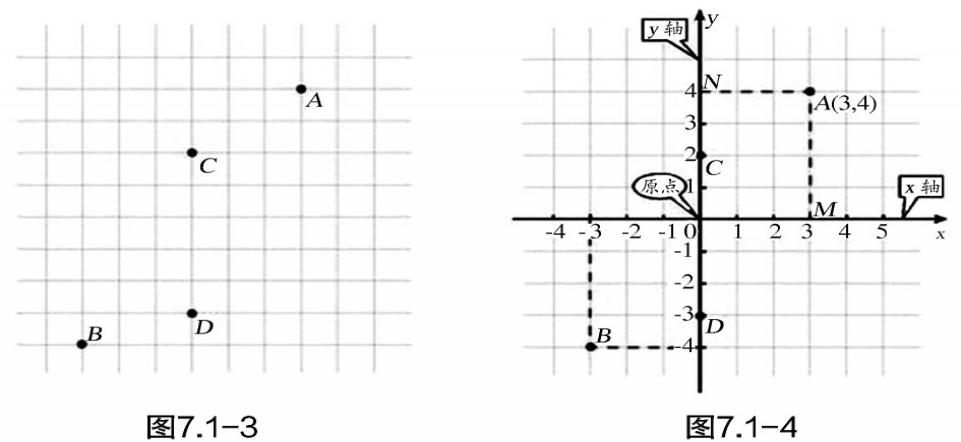
如图7.1-4，我们可以在平面内画两条相互垂直、原点重合的数轴，组成平面直角坐标系（rectangular coordinate system），水平的数轴称为x轴（x-axis）或横轴，习惯上取向右为正方向；竖直的数轴称为y轴（y-axis）或纵轴，取向上方向为正方向；两坐标轴的交点为平面直角坐标系的原点。

有了平面直角坐标系，平面内的点就可以用一个有序数对来表示了。例如，如图7.1-4，由点A分别向x轴和y轴作垂线，垂足M在x轴上的坐标是3，垂足N在y轴上的坐标是4，我们说点A的横坐标是3，纵坐标是4，有序数对（3，4）就叫做点A的坐标（coordinate），记作（3，4）。类似地，请你写出点B，C，D的坐标：B（______，______），C（______，______），D（______，______）。

基本要求：

（1）要有板书；

（2）试讲10分钟左右；

（3）条理清晰，重点突出；

（4）学生能够在直角坐标系中表示点。

答辩题目：

1. 画平面直角坐标系时要注意什么？

2. 平面直角坐标系把坐标平面上的所有点分成几大类？

试讲答案：

各位考官：大家好，我是初中数学组的XX号考生，我试讲的题目是《平面直角坐标系》，下面开始我的试讲。

一、复习旧知，导入新课

师：同学们都知道数轴上的点与实数是一一对应的。数轴上的每个点都对应一个实数，这个实数叫做这个点在数轴上的坐标，试着表示出这个数轴上点A，B，C的坐标。

师：A点坐标为-4，B点坐标为2，C点坐标为5。

师：在电影院里你是如何找到自己的座位的？

师：对，电影票上标有X排X座，所以找座位时，先找第几排，再找这一排的第几座就可以了。

师：电影院里的座位必须由两个数才能确定下来。实际上，生活中有很多时候需要用一对数字确定平面内一点位置。你能举出一些例子吗？

师：同学们回答得很好，像电影票上的座位、中国象棋棋盘上的棋子位置、自己所在的班级位置等都是由两个数确定的。

师：是的，平面内点的位置的确定需要两个数，而借用一条数轴只能确定直线上的点的位置，那么对于平面内的点我们需要借用几条数轴来确定它的位置呢？

二、探索新知，解决问题

师：类似于利用数轴确定直线上点的位置，你能不能找到一种方法来确定平面内的点的位置呢？观察平面内各点的位置，你发现了什么？

师：学生A说平面内的每个点都可以由水平线和竖直线相交的点表示。

师：用数轴代替这两条水平线和竖直线，并且原点重合，试着画一画。

师：怎样画才能把平面内的A点准确无误的表示出来呢？

师：学生B说要画两条互相垂直的、原点重合的、具有相同长度单位的数轴。

师：在平面内，两条互相垂直且有公共原点的数轴组成平面直角坐标系。我们把水平方向的数轴称为x轴或横轴，向右为x轴正方向；竖直方向的数轴称为y轴或纵轴，向上为y轴正方向；公共原点称为坐标原点。

师：这个平面直角坐标系是由笛卡儿发明的，所以我们还把它称为笛卡儿坐标系。

师：请大家分别由A点向x轴和y轴作垂线，垂足分别为M，N，你能得出什么吗？

师：学生C说M点在x轴上的坐标是3，N在y轴上的坐标为4。

师：这样我们就得到了一个有序数对（3，4），就叫做A点的坐标，记作A（3，4）。

师：类似地，你能表示出点B，C，D的坐标吗？

师：学生D说B点坐标是（-3，-4），C点坐标是（0，2），D点坐标是（0，-3）。

师：都对了。像这样的有序实数对叫做点的坐标，横坐标写在纵坐标前，点的坐标通常与表示该点的大写字母写在一起。

三、例题巩固，深化理解

师：在平面直角坐标系中描出点E（4，5），F（-2，3），G（-4，-1），P（-4，-2），Q（2.5，-2），看看谁描得最快，谁描得正确得最多！

四、小结作业

师：请大家回忆一下这节课都学了什么？课后大家预习一下象限的知识。

师：好，下课，同学们再见！

五、板书设计

平面直角坐标系

x轴，y轴，坐标原点

互相垂直

我的试讲到此结束，谢谢各位考官的聆听。

答辩答案：

1. 学生在学习平面直角坐标系时，对其正方向、原点、单位长度等概念有时候会不够清晰。因此要注意引导学生明晰平面直角坐标系中两坐标轴之间成直角，交点为原点，向右为x轴正方向，向上为y轴正方向。

2. 因为平面直角坐标系把坐标平面分成四部分，分别为第一象限、第二象限、第三象限、第四象限。但是坐标轴上的点不属于任何象限。所以，坐标平面上的点可以被分成五大类，各象限内的点与坐标轴上的点。

☟☟☟

添加教师资格客服老师微信

备注“网站”

获取更多考试资讯和海量备考干货

2024教资上岸大本营

• 考试公告
• 成绩查询
• 资格认定
• 备考讲座

扫码进群，备考路上不孤独，互帮互助，共同上岸！

点击打开